PARTICLE IN A BOX:  VISIBLE SPECTRA OF DYES

 

            Schroedinger developed quantum mechanics based on the use of classical wave equations to describe subatomic particles.  One form of the Schroedinger equation for a particle moving in one dimension is

 

 

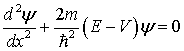
where

                        y  =  wave function (No physical meaning, but y2 proportional to

                                 probability of finding particle.)

 

                        m  =  mass of particle

 

                        E  =  total energy

 

                        V  =  potential energy

 

 

            The “particle-in-a-box” is a description of a small particle moving in a box in which the potential energy, V, is zero in the box, but is infinite outside the box.  The length of the box is “a”.

 

 

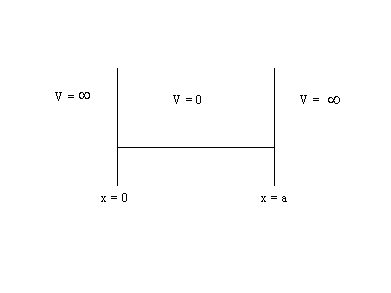
            In order to keep the particle in the box y must be zero outside the box.  Because y must be continuous, y must also be zero at  and .

 

            One solution to this problem is

 

 

 

 

 

 

 

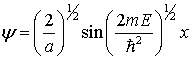
At , ; thus

 

 

 

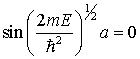
But also

 

Where

 

So,

 

 

 

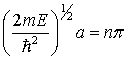
or

 

 

 

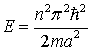
or

 

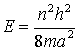
(n is a quantum number 1, 2, 3, ...)

 

 

 

            According to our results, the energy levels are quantized!

 

            The Pauli exclusion principle requires that there be no more than two electrons in any energy level.  For molecules with N p electrons there will be N/2 levels.  If an electron jumps from the level n = N/2 to the lowest empty level, N/2 + 1, the change in energy,    , is

 

 

 

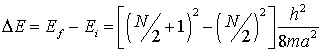
Since

 

Where

 

n = frequency

c = speed of light

l = wavelength

 

 

 

 

or

 

 

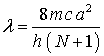
            For the series of compounds we will study

 

 

where j is the number of double bonds in the polyene chain between two rings and  the C---C bond length of order 1.5.

 

            Also N = 2j + 4.  In addition the highly polarizable benzene rings require that we increase the length of the box by L.

 

So that

 

 

or

 

Then

 

 

 

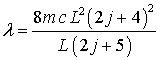
            By increasing the box length by L

 

 

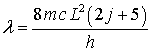
            The above equation may be used to estimate the wavelength of light absorbed by an electron of mass, m, in a polyene chain.

 

 

 

 

PURPOSE

 

            The purpose of the experiment will be to test the particle-in-a-box model.  For an  electron in a box the wavelength of maximum absorption is given by

 

 

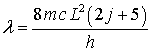
EQUIPMENT AND CHEMICALS

 

            Spectrophotometer (Turner 350, Coleman 124, P. E. Lambda 3)

            Methanol

            Cyanine dyes ( stock solutions in methanol, referred to as

                        #I, #II, #III.)

 

 

Compound (I)

 

1,1’-DIETHYL-2,2’-CYANINE IODIDE

 

Compound (II)

 

 

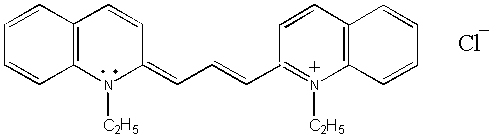
1,1’-DIETHYL-2,2’-CARBOCYANINE CHLORIDE

 

Compound (III)

 

(III)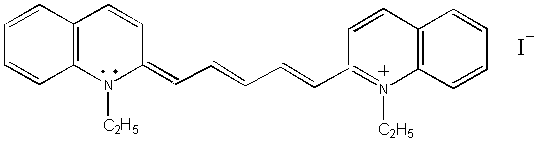

1,1’-DIETHYL-2,2’-DICARBOCYANINE IODIDE

 

            #II is also known as pinacyanol chloride.

 

 

 

 

PROCEDURE

 

            From  stock solution, prepare the following solutions (Use 100 microliter micropipet.)

 

            #I         Dilute 0.10 ml to 10 ml in methanol

                        Dilute 0.10 ml to 25 ml in methanol

 

            #II        Dilute 0.10 ml to 25 ml in methanol

                        Dilute 0.10 ml to 50 ml in methanol

 

            #III        Dilute 0.10 ml to 25 ml in methanol

                        Dilute 0.10 ml to 50 ml in methanol

 

            For each dye you will have two solutions of different concentrations.  Scan each solutions as follows:

 

            #I         470 - 550 nm

 

            #II        575 - 635 nm

 

            #III        675 - 735 nm

 

Use the graph showing absorbance (A) vs. wave length (l) for each solution.

 

            Use Beer’s law to determine the molar absorptivity for each solution of each dye.

 

                       

 

                        A = Absorbance

 

                        a = molar absorptivity

 

                        b = path length in cm

 

                        c = concentration, mol/L

 

For each solution calculate a.  For a given dye the two values of a should agree within five per cent.

 

 

 

            For each dye calculate maximum l for the electron-in-a-box and compare it with your experimental values.

 

            Literature values for maximum l are the following:

 

                        Dye #I             525 nm

                        Dye #II            610 nm

                        Dye #III            705 nm

 

(From Introduction to Quantum Concepts in Spectroscopy, W. G. Laidlow, 1970, p. 35.)