DATA PROCESSING

Precision and Accuracy

There is some degree of uncertainty associated with every physical measurement. In order to express the reliability of measurements, the terms accuracy and precision are used. Accuracy is a measure of the agreement of a measured value with the true or accepted value. The true value is seldom known, except by definition or agreement. Hence, precision is often a better measure of reliability. Precision is the agreement of several measurements with each other and is concerned with the reproducibility of measurements. Generally, it can be assumed that better precision indicates a higher probability of the date being accurate.

Significant Figures

A rough estimate of precision an be shown with significant figures. These are all the figures which are known with certainty. For example, suppose you are measuring temperature with a thermometer calibrated in degrees centigrade. If the temperature is indicated to 21°, we know that it is 21°, not 20° or 22°. The uncertainty is generally assumed to be one-half of the last indicated place. Thus 21° is actually 21 + 0.5°. With a thermometer calibrated in hundredths of degrees the temperature might be recorded as 21.37 + .005°.

Measurements may be expressed in different units. For example, a length might be 0.026m or 2.6cm or 26mm. When using different units, it is customary to express the number in exponential or scientific notation. The digits express the number of significant figures, while the exponent serves to locate the decimal point. We write 2.6cm as nm, not as 26,000,000 nm.

Zeros may or may not be significant. In the number 0.026 the zeros are not significant. They only locate the decimal point. But in the number 0.0260 the last zero is significant. In 260mm the zero may or may not be significant. Again to avoid confusion, 260 should be written as or .

Errors

Errors associated with measurements are usually divided into two types: systematic errors and random errors. In principle, systematic errors can be corrected or eliminated, since they involve errors in technique or method. Common systematic errors include instrument errors (calibration or adjustment), reagent error(impurities or change in concentration), and calculation errors (failure to use correct equation or theory; these are not mathematical mistakes). In many cases systematic errors are not detected and, thus, not corrected. Since most systematic errors are reproducible, they effect the accuracy of the measurement, but not the precision.

Random errors are those which can be reduced with proper care, but which cannot be eliminated. Since random errors effect reproducibility, they influence both precision and accuracy. Common random errors include titration errors, proper draining of buret, removing last drop from tip, and judging the correct color at the end point, weighing errors, judging the level of liquid in volumetric glassware, and parallax error in reading instruments and volumetric glassware.

Error can be expressed as an absolute error or relative error. The absolute error can be defined as

Where O is the observed value and A is the accepted value.

The relative error may be defined as

Relative error may be expressed as per cent, 100 E_r, or parts per thousand, 1000 E_r.

Statistical Analysis of Data

Measures of central tendency (mean, median, and mode) serve as reference points for interpreting date. The purpose of measures of central tendency is to show where the typical or central values lies within a group.

The most common measure of central tendency are the following:

1. Arithmetic mean - also referred to as simple the mean or the average.

The mean, , of N values, is given by

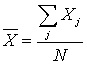
2. Median - the midpoint of a distribution.

3. Mode - the most frequent value in a distribution.

It is generally recognized that the mean is the best measure of central tendency. However, if there are some extremely high or low values in a distribution, it may be advisable to use the median.

In addition to knowing the central tendency of a distribution, it is also necessary to know the spreading out or dispersion of data. The most commonly used measures of dispersion are average deviation and standard deviation.

The average deviation, a, is the average of the deviations from the mean.

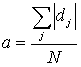
where is the deviation,

The standard deviation, , is the square root of the average of the squares of the deviation,

When N is small, less than 30, it is better to use N-1 in computing the standard deviation. In large samples, it makes little difference which one is used.

Computer Analysis

Several statistical programs are available on the TRS-0 and PET micro-computers and the DSU timesharing terminals. You are encouraged to use these and to learn BASIC programming. However, if the computer does your calculations, be sure you know what the computer is doing.