|
| |
INTRODUCTION TO STATISTICAL ANALYSIS
Hypotheses Testing
a. The common approach to testing a hypothesis is to establish a set
of two mutually exclusive and exhaustive hypotheses about the value in
question. For example:
Ho: Mean = 10 pounds
Ha: Mean does not equal 10 pounds
b. Next we perform our statistical analysis (perhaps in this
particular example we are testing that the mean weight loss from a new
diet drug is 10 pounds). If our statistical analysis is found to be
significant then we reject the null hypothesis (Ho) and find that the
mean does not equal 10 pounds.
c. Occasionally, the hypotheses will be directional (also known as a
one-tail test). For example:
Ho: mean = 10 pounds
Ha: mean > 10 pounds
d. When we write hypotheses we normally hope to reject the null
hypothesis and find that there is a difference. The exception to this
being in some forms of multivariate data analysis it is required to
accept the null hypothesis in order to test the assumptions of the
statistical technique. For what we are doing in this course the proper
course of action will be to reject the null hypothesis.
How do we determine when we can reject or accept a null hypothesis? The
answer lies in examining the significance level, labeled as alpha (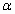 ). ).
e. The significance level is normally labeled as "p value" and is
often reported in statistical reports. Researchers must report their
significance level a-priori (prior to conducting the statistical test).
f. If we wait until after we have conducted the statistical tests,
the results do not change but it would be comparable to deciding what is
a good and passing grade on an exam after the exam has been graded. It
can be done, but it is not recommended.
g. There are three common significance levels that we use in
statistical analysis (.10, .05, and .01). If we split this significance
into the two-tails of the curve then we have what is known as a
two-tailed (non-directional) test. We will discuss this more in the
coming weeks.
h. We test whether we have met the required level of significance by
comparing the statistical value that we compute with a known table of
critical values.
i. If the calculated value is greater than the value within the
table of critical values, then we reject the null hypothesis.
ii. If the calculated value is less than the value within the
table of critical values, then we fail to reject (some statisticians
indicate that they accept) the null hypothesis.
i. What does the significance level tell us? The significance level
tells us how likely we are to make an error when we reject the null
hypothesis. If we are testing at the .10 level then we are saving that
10% of the time (10 times out of 100) we will incorrectly reject the
null hypothesis when we should have failed to reject (accept)
i. This concept becomes more important if we consider the various
possibilities for statistical research, and the researcher must take
very seriously the level he or she will set alpha.
ii. If we are conducting research on finances, then it is
probably acceptable to use the .10 level. After all, if we are
testing whether a given investing technique will increase our mean
earnings, then there is little physical harm if we reject the
technique when we should have accepted it.
iii. However, if we are conducting life-saving research on a new
drug, then are we willing to reject the use of a drug that could
save someone’s life? Probably not, we may want to test at a more
restrictive level.
Types of Error
j. Type I Error – this is where the researcher will reject the null
hypothesis when he or she should have accepted the null. Symbolized as
Alpha (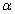 ). ).
k. Type II Error – this is where the researcher will accept the null
hypothesis when he or she should have accepted the null. Symbolized as
Beta (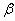 ) )
l. The two types of error are inversely related. As Type I error
increases, Type II error decreases; and likewise, as Type I error
decreases, Type II error increases.
m. Prior to conducting research, the issue of error must be
considered and the researcher will have to determine which type of error
is considered more acceptable. For simplification of this concept see
the table below:
|
Conclusion of Statistical Test |
Ho is true |
Ho is false |
|
Ho is not rejected
|
Correct Conclusion |
Type II Error |
|
Ho is rejected
|
Type I Error |
Correct Conclusion |
The Issue of Power
n. The term power refers to the ability of a statistical test to
reject a false null hypothesis. Thus, it is obvious that we want to
create powerful research designs. We have already discussed that the
probability of a type I error is called alpha, and is usually set at
.05, .01, or .001.
o. Another convention is to set the probability of making a type II
error at .20. This convention demonstrates that most researchers are
less concerned with making a type II error than they are with making a
type I error. Power is defined as 1 - b . So
if b = .20 then power is equal to .80. If
this level of power cannot be achieved in an experiment, then a failure
to reject the null could mean that no relationship exists within the
population, or that the design was simply too weak to detect a real
difference.
p. Power is affected by several considerations:
i. Sample size. As sample size increases, so do does the power of
the study.
ii. Alpha level. As alpha is increased, Beta is decreased,
therefore increasing power.
iii. Direction of the test. A one tail test is more powerful than
a two tail test.
iv. Effect size. As effect size increases, power increases.
Assumptions of Statistical Tests
q. Each test that we will discuss will have its own assumptions.
While a violation of an assumption does not mean that you cannot use the
statistical technique, multiple violations could present a problem.
r. Many of the assumptions are the same across most of the
statistical techniques that we will study.
i. Parametric statistics – statistics that require normal
distribution
ii. Nonparametric statistics – statistics that do not require
normal distribution
|
![]() ).
).