Lecture Outline

STATISTICS

The importance of distributions

a. Allow for social scientists to organize data that possibly could not have been interpretable without the organization.

b. Distribution means the ordering of data in order of magnitude

i. Frequency distribution allows the researcher to see more general trends than he or she could with an unordered set of data

ii. Frequency distributions are also significantly more compact and therefore take up less space when we write them up

iii. Frequency distribution looks like the following:

x	f
10	1
8	1
7	3
6	3
5	2
4	1
3	1

c. The easiest way to examine frequencies is through the use of graphing. There are two types of graphs that I would recommend:

i. The histogram – here a bar is drawn for each raw score, with the height of the bar representing the frequency the score occurs

ii. The asterisk graph – here the raw score is presented on the left of the graph and one asterisk is placed in the second column for each occurrence of the value (these asterisks go across horizontally). These graphs allow us to visually see how our data is falling in relation to all of the values.

Measures of central tendency

d. These are measures designed to give information concerning the average or typical score within a larger set of scores. For example suppose we want to test the average IQ for prisoners housed in the disciplinary unit at Parchman. We would use one of the soon to be discussed methods of examining the average or typical inmate’s IQ.

e. There are 3 measures of central tendency that we will talk about (Mean, Median, and Mode).

i. Mean – The mean is the most commonly used measure of central tendency because it is the best mathematical calculation of the average. It is denoted as either capital "M" or as "", also known as X-bar.

1. The mean is calculated using the following equation: 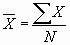. This equation is read as the mean is equal to the sum of all X values (raw scores) divided by the number of cases in the study. The use of capital letters versus lower-case is important and should be considered because a lowercase "n" would stand for only the subjects in one group, where capital "N" stands for all subjects in a study. Here there is no difference but in later sections there will be a difference between the two.

2. The mean is the most often used but can be susceptible to extreme scores termed "outliers", or scores that are extremely unusual and outside the normal range of scores in the study.

3. Interpretation of the mean must be conducted carefully as the difference between groups could impact the difference between mean scores.

ii. The Median – this is the exact midpoint of any distribution and is where 50% of the cases will fall above and 50% will fall below. The median is used less than the mean because it is not as mathematically computed. The median is denoted as "Mdn".

1. To calculate the median, one has to arrange the data in distribution form in the order of magnitude. Then count up to the middle point in the distribution.

2. If there are an odd number of cases in the study, for example 9, then the median would be the 5^th value.

3. If there is an even number of cases in the study, for example 8, then the median could be computed by taking the 4^th and 5^th scores and dividing by 2.

4. This measure is less susceptible to the presence of outliers and extreme scores.

iii. The Mode – this is the most commonly occurring score in a distribution and is symbolized as "Mo".

1. If we have a frequency distribution developed, then we merely have to look for the score with the highest "f" value. If we have a histogram or asterisks graph then we merely have to look for the score under the tallest bar or the longest asterisk.

2. If we do not have a graph or a frequency distribution, then we have to order the data and then attempt to see which occurs most frequently.

3. Occasionally, you may find a set of scores that has more than one mode. In this case you have what is known is a bimodal distribution if there is 2, or a multimodal distribution if there is more than 2. Here, you many find that two separate groups have been classified together. For example, in a study concerning the number of hours inmates spend with family members during visitation, you may have accidentally grouped minimum security (who receive less limited access) and maximum security (who are limited) together in the same study.

Why do we need to understand all 3 measures? Because occasionally we may encounter a distribution that is skewed.

f. The normal distribution – this is the perfect distribution of scores. There are an equal number of cases falling both above and below the middle point of the curve. In this situation, the mean, median, and mode all fall at the same point.

g. Skewed distributions – this occurs when extreme scores pull the mean away from the middle point of the distribution.

i. Negative skew – this is where the tail of the curve slopes to the left of the distribution. It is characterized by the mean of the data set’s scores being less than the median and the mode. In fact, the mean will be the smallest value, then will come the median (which is the center point) and then will come the mode (which is characterized by the large hump on the curve).

ii. Positive skew – this is where the tail of the curve slopes to the right of the distribution. It is characterized by the mean of the data set’s scores being greater than the median and the mode. The mean is in fact the largest value, followed by the median (which is still the center of the distribution), and then the smallest number will be the mode (characterized by the large hump on the curve).

Measures of Variability

h. Just as the measures of central tendency allow us to examine the average of the scores, the measures of variability allow us to examine how much our scores vary. This variance is to be expected since we will rarely (hopefully never) encounter a study where everyone scores the same on a test or a subject of study. These measures then allow us to gain a better understanding of the true nature of the data sets. Consider the weather example given in class.

i. There are 3 measures of variability to discuss.

i. Range – this is the quickest and easiest method of calculating variability. It is also the least recommended because it is extremely influenced by extreme scores.

1. The range is calculated by subtracting the smallest score from the largest score in the distribution.

2. For example, if we have are examining the number of arrests and we have someone who has been previously arrested 30 times and we have someone who has been arrested 2 times, then our range is 28.

3. The range can also drastically change. It can never go down but it can continue to go up. If a new subject is added that had 40 arrests, then our range is now 38.

ii. Standard Deviation – this is considered the greatest measure of variability. Unlike the value for the range, the standard deviation takes into consideration all of the scores in a dataset. The standard deviation allows us to examine how much our scores vary around the mean. Because the mean is being considered in the standard deviation, the data used must be interval or ratio in nature. The standard deviation is denoted using one of two symbols "SD" or "s". There are two methods of computing the standard deviation.

1. The deviation method. Not considered the easiest but can be covered if there is an interest in this method.

2. The computational method. Here the standard deviation is calculated using the following formula: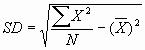

3. The use of the standard deviation allows us to determine exactly how much the scores vary around the mean. Suppose we develop two treatment programs that reduce the number of arrests a juvenile will suffer in their life. If we test program one and we get a SD of 2, and we test program 2 and get a SD of 8, then which program should we push to the administration?

iii. The Variance – this measure of variability is closely related to the standard deviation. In fact, it is merely the standard deviation squared, or it is the above formula without taking the standard root. We use two measures for the same concept because later on with advanced statistics we will rely on the measure of variance.

Z scores and the Normal Curve

j. The Normal Curve – this is the perfect bell-shaped curve where 50% of our cases fall below the mean and 50% of our cases fall above the mean. There are some common characteristics of the normal curve: the two halves are identical to each other and the measures of central tendency will all occur at the same point (in the very center).

i. We can standardize the normal curve and we will find that the mean will be 0 and the standard deviation units will be marked off in increments of 1. This is necessary because occasionally we may want to compare two separate groups. Without standardization we cannot because we would be comparing "apples and oranges".

ii. Still, 50% of the cases fall above and 50% fall below. So we can state the following: 34.13% of all cases fall between 0 and +1 and 34.13% of all cases fall between 0 and -1. Further 13.59% of all cases will fall between +1 and +2 and 13.59% of cases will fall between -1 and -2. Finally, 2.15% of cases will fall between +2 and +3 and 2.15% of cases will fall between -2 and -3.

iii. Now we can combine this information and state that 68% (a little more) of all cases will fall somewhere between + or – 1 standard deviation unit from the mean of the distribution.

iv. Therefore, if we have a sample of test scores with a mean of 75 and a standard deviation of 5, then we can state that 68% of our scores will fall between the score of 70 and 80. 95% of our scores will fall between 65 and 85. And 99% of our scores will fall between 60 and 90. The remaining 1% will fall either above or beyond 60 and/or 90.

k. Z scores – this value assists us in interpreting raw score performance since it takes into account the mean and the measures of variability (the standard deviation). The z score allows us to examine an individual’s score versus that of the rest of the distribution. We can also compare the individual’s performance on two separate normally distributed sets of scores.

i. Easy to calculate and then we merely refer to the table in the back of the book (Table III – Normal Distribution – p. 564). Positive z scores tell us the number of scores that fall above the calculated z score and negative z scores tell us the number of scores that fall below the calculated z score.

ii. Calculated by using the following formula:
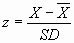