The T Test
The t test was named by William Gossett, who published his research under the pseudonym "student"; henceforth the reason the test is often referred to as the student’s t test. The t test is designed to compare differences between 2 groups with small sample sizes.
The t ratio (also referred to as the t value) is a ratio of the difference between 2 sample means and the population mean of the entire sampling distribution of differences to the estimated standard error of that distribution.
Formula for calculating t looks like this:
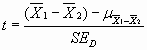
However, the value for ![]() should be equal to zero,
if the samples are drawn from the same population. These symbols indicate the
mean of the entire distribution of differences, which is zero because the mean
difference in the sample distribution will be zero if drawn from the same
population.
should be equal to zero,
if the samples are drawn from the same population. These symbols indicate the
mean of the entire distribution of differences, which is zero because the mean
difference in the sample distribution will be zero if drawn from the same
population.
ASSUMPTIONS OF THE T TEST
WHAT THE T TEST ALLOWS RESEARCHERS TO DO
The t test allows the researcher to test the means of two groups and determine if there is a statistically significant difference between the means of the two groups. Significance is determined by comparing the calculated t value with a known table of critical value. The table value is determined by considering the alpha level (generally .05 or .01) and the degrees of freedom (calculated as N-2).
The null hypothesis can be written a number of different ways depending upon whether we are conducting a one-tail test or a two-tail test. A one tail test is often referred to as a directional hypothesis and the two tail is referred to as non directional.
If the calculated t value is greater than the table t value then we reject the null hypothesis and find that there is a statistically significant difference. If the calculated t value is less than the table t value then we fail to reject the null hypothesis (or accept the null hypothesis depending upon your preference for statement).
For example, we arrive at the following information after we run calculations:
Calculated t = 3.321, df=11
Table value for t (two tail test) = 2.201
Table value for t (one tail test) = 1.796
Based upon this information we would reject either of the above null hypotheses and find that there is a statistically significant difference between the means for the two groups.
TWO TYPES OF T TEST WE WILL EMPLOY IN THIS COURSE
One-sample T test – here the researcher is attempting to compare the mean from a study sample group with an established population mean.
To analyze a one-sample t test on SPSS
Open the Data File
Select Analyze
Select Compare Means
Select One-sample T test
Move the variable of interest to the Test Variable box
The value for the test value is changed to the established mean we are testing against.
Click OK
Independent Group T test – here the researcher is attempting to compare the means of two different groups. For example, suppose I want to test whether there is a statistically significant difference between the mean scores on a pop quiz in Theories of Criminal Behavior. The two groups are exposed to two different teaching styles. Group One is provided one on one instruction, while group Two receives normal instruction. The researcher wants to see if there is any difference between the means of the two groups.
To analyze an independent group T test on SPSS
Open the Data File
Select Analyze
Select Compare Means
Select Independent samples T test
Move the variable that identifies the group to the Grouping Variable box
Click the Define Groups Box
| Enter the value to identify group 1 and the value to identify group 2 |
Move the dependent variable to the Test Variable box
Click OK
Then just interpret the printouts as we discussed in class..