Liquid-Vapor Equilibrium
Purpose
The purposes of this experiment are to measure
the vapor pressure of a pure liquid as a function of temperature and to
use that relationship to calculate the heat of vaporization.
Discussion
For any two phases in equilibrium, the free energies
must be equal
(8-1)
A small change in free energy in one phase must
be balanced by a corresponding change in the other phase.
(8-2)
but ;
so
(8-3)
This may be rearranged to give
According to the Second Law of Thermodynamics
(8-5)
Substituting into equation 8-4,
(8-6)
Now let us consider the liquid-vapor equilibrium.
Since the volume of a gas is much larger than that of the same mass of
liquid, we may assume that .
Let us also assume that the vapor behaves as an ideal gas; that is,
.
Thus equation 8-6 becomes
DH is now the enthalpy of vaporization. From calculus, we know that
(8-8)
and
(8-9)
So, we can rewrite equation 8-7,
(8-10)
When we plot
vs. x,
is the slope of the curve. If we plot
versus
, the
slope will be
.
Thus the heat of vaporization can be calculated
from Pressure-Temperature data.
In this experiment you will measure the boiling
point at various pressures.
Equipment and Chemicals
Cottrell-Ramsay-Young boiling point apparatus,
mercury, manometer, ballast bottle, and aspirator or vacuum pump, microburner,
barometer, hexane, cyclohexane, ethanol, or other volatile liquid.
Procedure
The apparatus should be assembled as shown in
Figure 8-1. Care should be taken to see that the system is air-tight.
Place some liquid in the boiling apparatus. Boiling
chips may be used to prevent bumping. Evacuate the system to the desired
pressure. Carefully heat the liquid to boiling. Avoid superheating and
see that the boiling liquid percolates over the thermometer bulb. Determine
the boiling pint at that given pressure. The pressure inside the system
is the atmospheric pressure minus the difference in height of the two mercury
columns in the manometer.
Add air to increase the pressure approximately
four cm. Again determine the boiling point. Repeat at other pressures to
get a wide range of pressures and temperatures.
Repeat with other samples of the same liquid.
CALCULATIONS
Plot a graph of
versus
. Determine
the slope and use equation 8-10 to calculate the heat of vaporization.
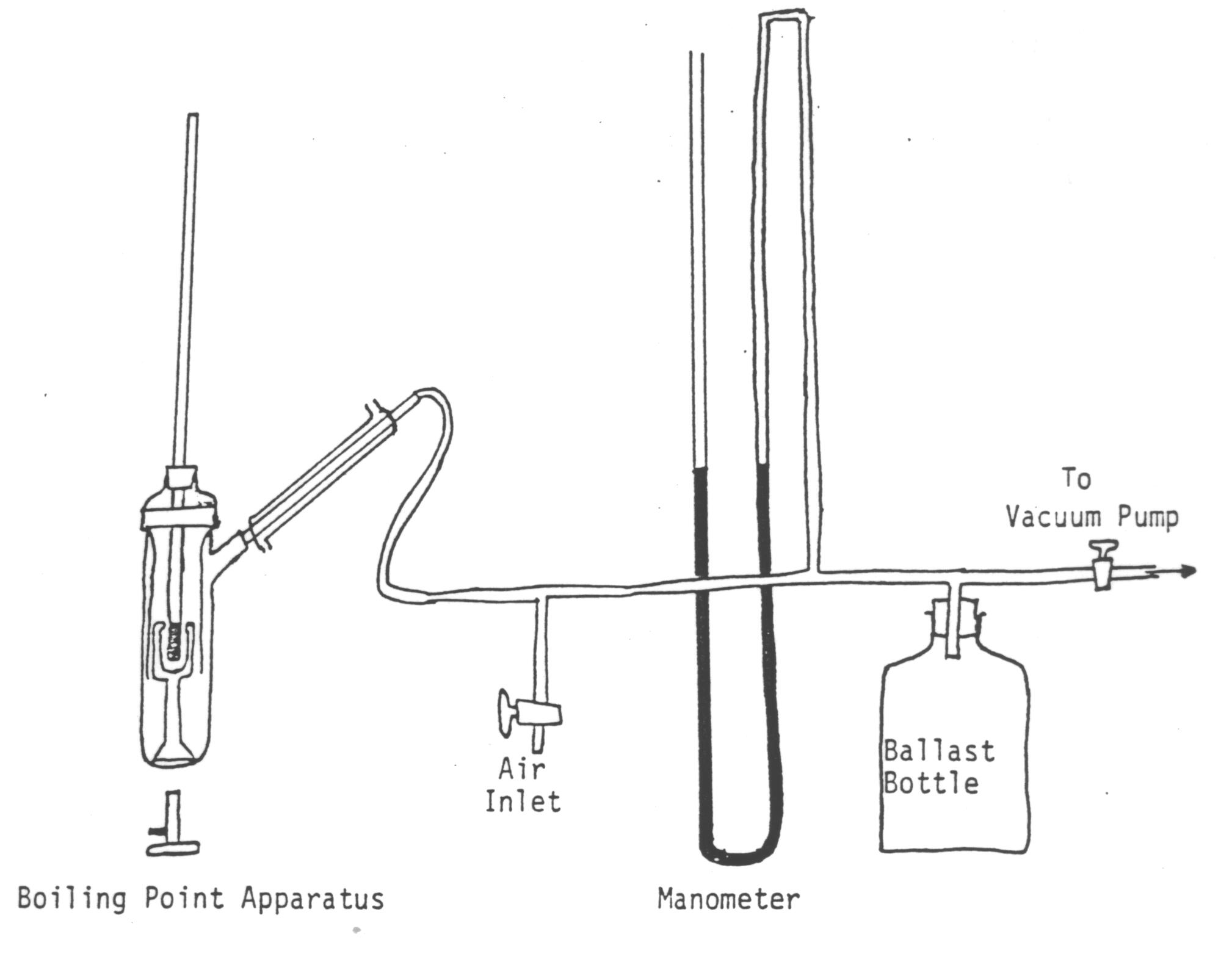
Figure 8-1. Cottrell-Ramsay-Young Vapor Pressure Apparatus
SAMPLE CALCULATIONS
Experiment: Enthalpy of Vaporization
Sample Data:
|
Pressure (mmHg) |
Boiling Pt. (oC) |
Boiling Pt. (K) |
ln P |
1/T (x 10-3 K-1) |
|
754.4 |
80.1 |
353.1 |
6.626 |
2.832 |
|
714.4 |
78.2 |
351.2 |
6.571 |
2.847 |
|
674.4 |
76.5 |
349.5 |
6.514 |
2.861 |
|
634.4 |
74.45 |
347.45 |
6.453 |
2.878 |
|
594.1 |
72.5 |
345.5 |
6.387 |
2.894 |
Calculations: Performing a linear regression
gives the slope and y-intercept for the line of best fit through the data.
For the above data, the slope is -3844.75 K. Thus, the value for the Heat
of Vaporization (DHvap)
of cyclohexane is determined to be:
DHvap = - (slope) x R = -(-3844.75 K) x 8.314 J/K mol
= -31965.25 J/mol